Länge har man haft idén att atomkärnan ungefär är som en vattendroppe, och skjuter man en neutron på den så delas den i två bitar, men exakt hur det går till har debatterats sedan 1930-talet [1].

Eftersom man inte kan lösa tidsberoende Schrödingerekvationen med, som i uranfallet, runt 230 växelverkande nukleoner, är forskarna tvingade att med hjälp av intuition och experiment finna drastiska approximationer för att förenkla problemet. En sådan modell lanserades 2011 [2] där kärnans rörelse antogs vara väldigt dissipativ vilket innebär att även om Coulomb kraften driver kärnan mot att delas så får rörelsen aldrig någon fart eftersom den kollektiva rörelseenergin hela tiden sprids till andra frihetsgrader. Dessa förenklande antaganden leder till en beskrivning av dynamiken baserat på den så kallade Smoluchowski ekvationen. Ett flertal arbeten har sedermera tillkommit baserade på liknande principer och som ger mycket bra beskrivningar av experiment, speciellt när det gäller fördelningarna av massorna hos fissionsfragmenten [3,4].

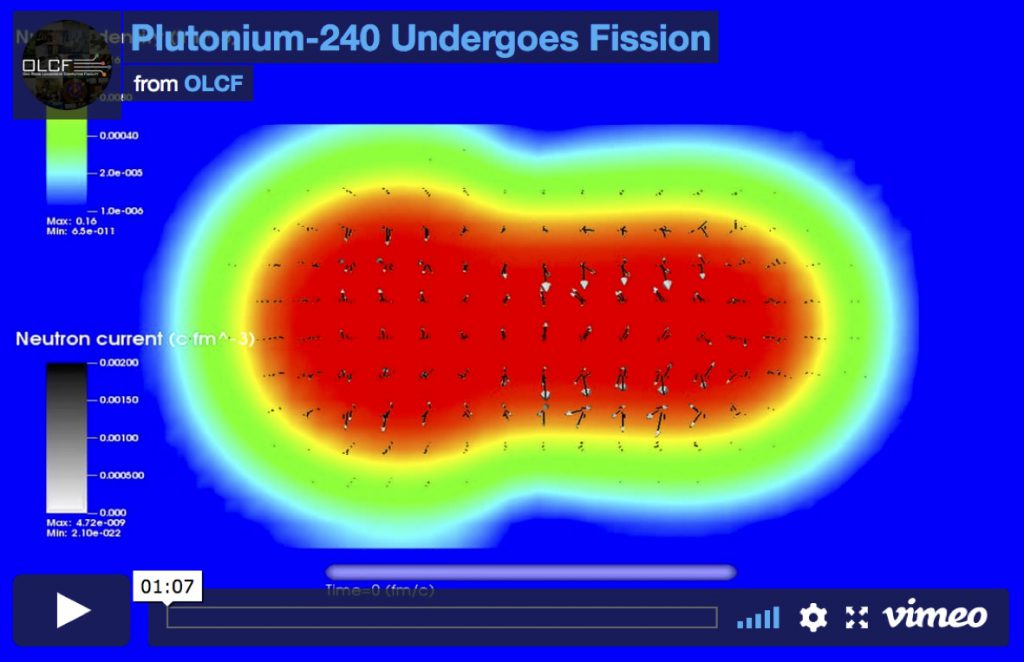
Nyligen lyckades forskare med hjälp av en annan approximation som kallas täthetsfunktionalteori simulera den sista biten av plutoniumkärnans väg till att delas. Dessa beräkningar är oerhört datorkrävande och utfördes på ett datorsystem bestående av 1760 grafikkort. En film som visar en av simuleringarna kan ses genom att klicka här. Resultaten är väldigt intressanta och stödjer idén att dynamiken är dissipativ [5,6].

Debatten om mekanismerna bakom fissionsprocessen kommer att fortgå men för tillfället talar en hel del för att kärnan rör sig med mycket dissipation ungefär som en klump sirap när den delar sig. Det kan tyckas förvånande eftersom kärnan i grundtillståndet är supraflytande med låg viskositet, men det är just förståelsen av det kontraintuitiva som är en del av tjusningen med fysik.

Gillis Carlsson
Ordförande för sektionen för kärnfysik

Referenser

[1] N. Bohr and J. A. Wheeler, Phys. Rev. 56, 426 (1939)

[2]  J. Randrup and P. Möller, Phys. Rev. Lett. 106, 132503 (2011)

[3] M. D. Usang, F. A. Ivanyuk, C. Ishizuka and S. Chiba, Scientific Reports 9, 1525 (2019)

[4] J. Randrup and P. Möller, Phys. Rev. C. 88, 064606 (2013)

[5]  A. Bulgac, P. Magierski, K. J. Roche, and I. Stetcu, Phys. Rev. Lett. 116, 122504 (2016)

[6]  A. Bulgac, S. Jin, K. J. Roche, N. Schunck and I. Stetcu, arXiv:1806.00694 (2019)